在梯度下降演算法中,求代價函數最小值時,是通過求導數來獲得。因此對於代價函數的每個參數,我們都需要分別求出各自的偏微分,如果參數越多,也就是特徵越多的問題,我們可以用矩陣運算的方式來取代求導函數。
這種方式就稱為正規方程,其定義如下: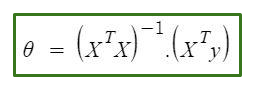
X代表特徵向量矩陣
X^T為矩陣X的轉置矩陣
(X^T*X)^-1為X的轉置矩陣和X矩陣相乘後的逆矩陣。
Y是訓練數據中的結果矩陣。
一般來說,特徵的數量決定了我們求解時是用梯度下降法或是正規方式,當n<1000時正規方式的效率較佳,但是當n>1000時,使用梯度下降法的方案會更好。
| 梯度下降 | 正規方程 |
|---|---|
| 需要學習率α | 不需要學習率 |
| 需求進行疊代運算 | 不需要疊代 |
| 對多特徵值的問題適應性較好 | 時間複雜度為O(n^3),不適合特徵數量n>1000的問題 |
| 可以應用到更複雜的演算法,如邏輯回歸 | 特徵向量的逆矩陣不存在時無法使用 |
